PSTAT 5A: Conditional Probability Continued & Bayes’ Theorem

Lecture 6

Author

Narjes Mathlouthi

Published

July 29, 2025

Today’s Learning Objectives

By the end of this lecture, you will be able to:

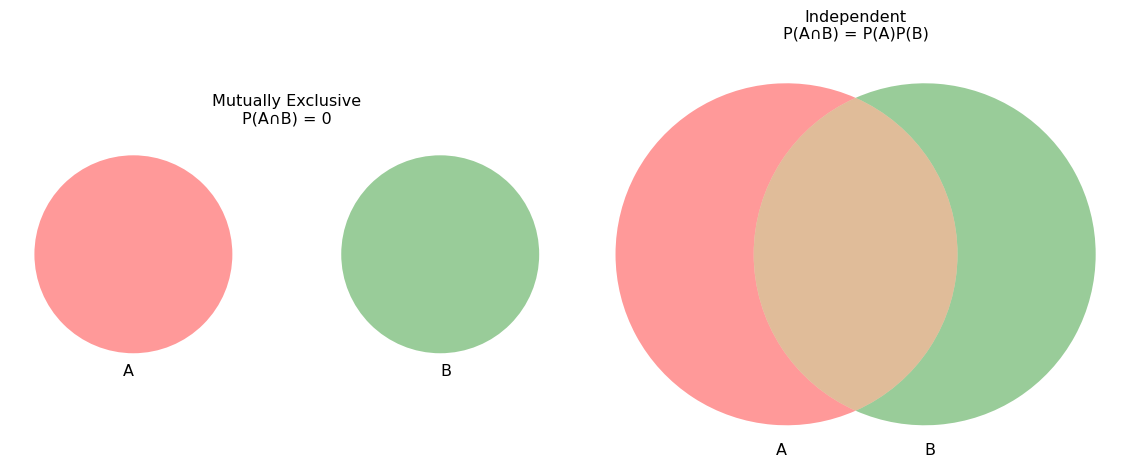
Mutually Exclusive vs. Independent

  • Mutually Exclusive (left): the circles A and B do not overlap, so \(P(A\cap B)=0\).

  • Independent (right): the circles overlap, and we’ve sized the intersection so that \(P(A\cap B)=P(A)\,P(B)\).

Mutually Exclusive vs. Independent Example

Draw a single card from a 52-card deck:

  • Let A={“draw an Ace”}, so P(A)=4/52.

  • Let B={“draw a King”}, so P(B)=4/52.

Q: What is \(P(A\cap B)\) ?

Solution. They’re disjoint (you can’t draw an Ace and a King), so \(P(A\cap B) = 0\).

But \(P(A)\,P(B) = \frac{4}{52}\times\frac{4}{52} = \frac{16}{2704} \neq 0\).

Hence, \(P(A\cap B)\neq P(A)P(B)\), so they’re not independent.

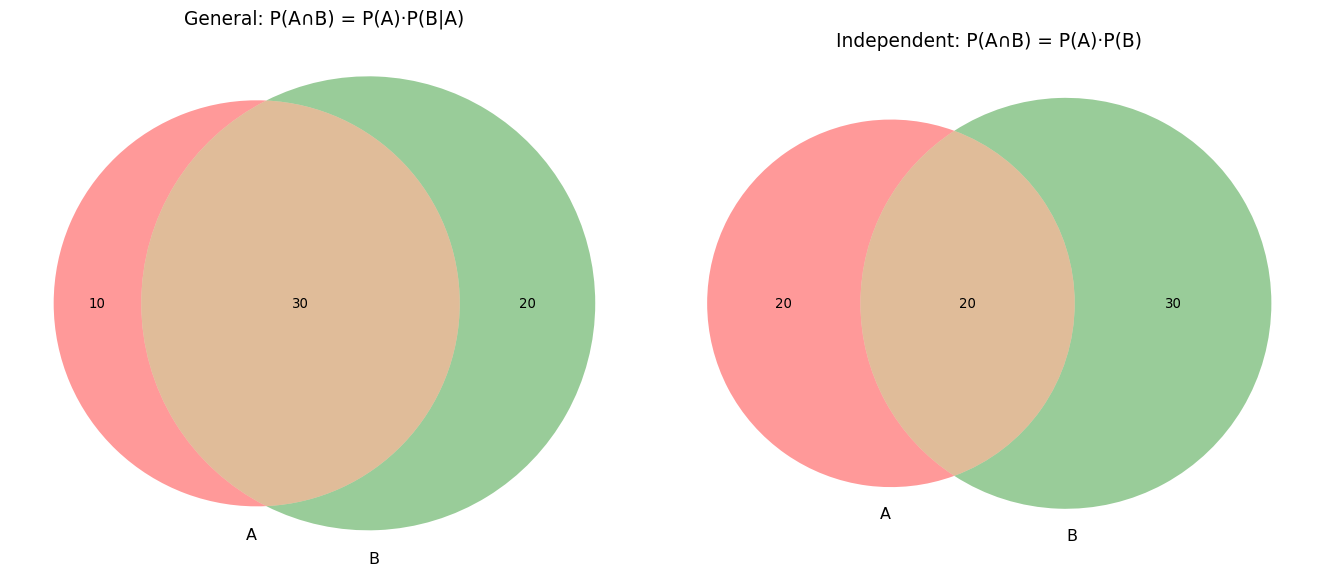
Multiplication Rule

General case: \(P(A \cap B) = P(A) \times P(B|A)\)

Independent events: \(P(A \cap B) = P(A) \times P(B)\)

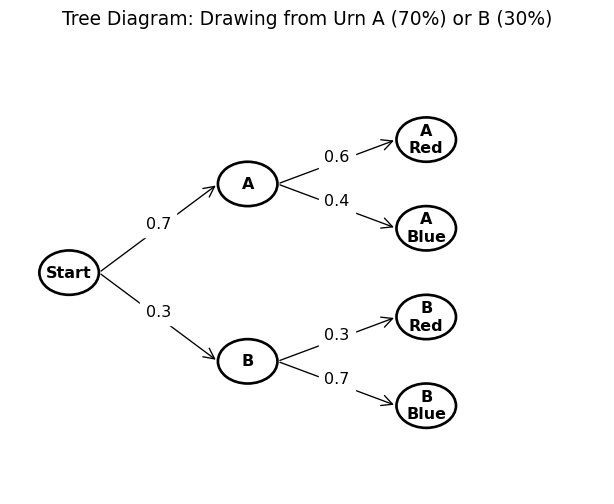
Tree Diagrams

🎯 Definition Tree diagrams help visualize sequential events and calculate probabilities.

Tree Diagram Examples

Practice Problem 2

A jar contains 5 red balls and 3 blue balls. Two balls are drawn without replacement.

  1. What’s the probability both balls are red?

  2. What’s the probability the first is red and second is blue?

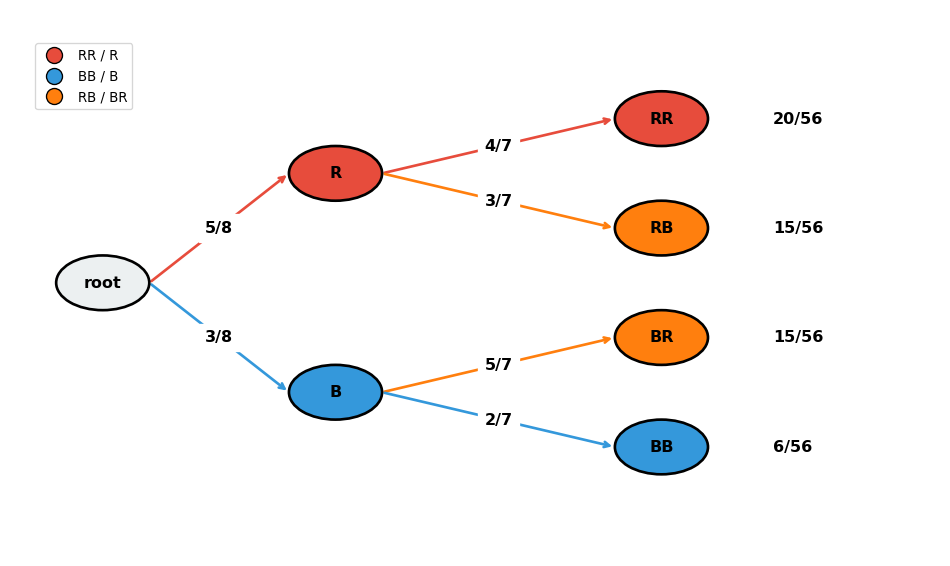
Solution.

  1. \(P(\text{both red}) = \frac{5}{8} \times \frac{4}{7} = \frac{20}{56} = \frac{5}{14}\)

  2. \(P(\text{red then blue}) = \frac{5}{8} \times \frac{3}{7} = \frac{15}{56}\)

Law of Total Probability

🎯 Definition

If events \(B_1, B_2, \ldots, B_n\) form a partition of the sample space, then:

\[P(A) = P(A|B_1)P(B_1) + P(A|B_2)P(B_2) + \cdots + P(A|B_n)P(B_n)\]

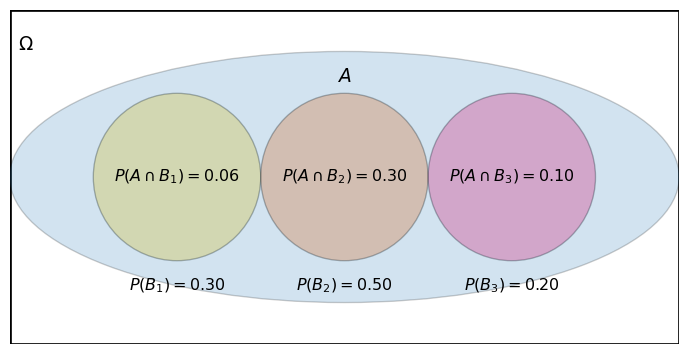
Law of Total Probability Example

A factory has two machines:

  • Machine 1: Produces 60% of items, 5% defective

  • Machine 2: Produces 40% of items, 3% defective

Q: What’s the overall probability an item is defective?

Solution. \(P(\text{defective}) = P(D|M_1)P(M_1) + P(D|M_2)P(M_2)\)

\(= 0.05 \times 0.6 + 0.03 \times 0.4 = 0.03 + 0.012 = 0.042\)

Bayes’ Theorem

🎯 Definition \[P(A|B) = \frac{P(B|A) \times P(A)}{P(B)}\]

This allows us to “reverse” conditional probabilities

Named after Thomas Bayes (1701-1761)

Bayes’ Theorem Components

  • \(A,B\): Events
  • \(P(A|B)\): Posterior probability - what we want to find
  • \(P(B|A)\): Likelihood - given \(A\), probability of observing \(B\)
  • \(P(A)\): Prior probability - initial probability of \(A\)
  • \(P(B)\): Marginal probability - total probability of \(B\)

Bayes’ Theorem Example

Medical test for a disease: 1

  • Disease affects 1% of population

  • Test is 95% accurate for sick people

  • Test is 90% accurate for healthy people

Q:If someone tests positive, what’s the probability they have the disease?

Bayes’ Theorem Solution

Let:

  • \(D\): Person has disease

  • \(T^+\): Test is positive

Given:

  • \(P(D) = 0.01\)

  • \(P(T^+|D) = 0.95\)

  • \(P(T^-|D^c) = 0.90\), so \(P(T^+|D^c) = 0.10\)

Solution. \(P(T^+) = P(T^+|D)P(D) + P(T^+|D^c)P(D^c)\)

\(= 0.95 \times 0.01 + 0.10 \times 0.99 = 0.1085\)

Bayes’ Theorem Solution (cont.)

\[P(D|T^+) = \frac{P(T^+|D) \times P(D)}{P(T^+)} = \frac{0.95 \times 0.01}{0.1085} \approx 0.088\]

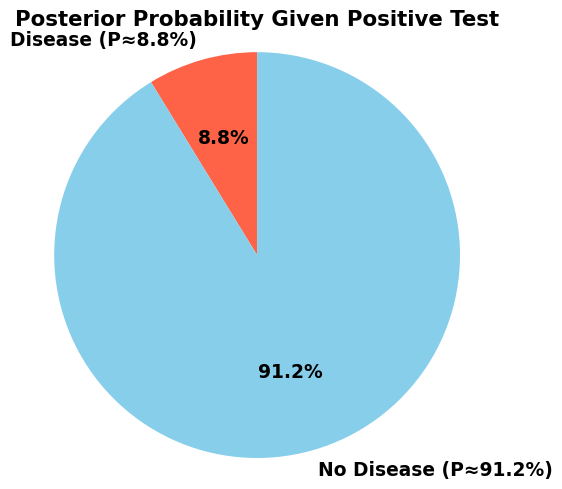
Surprising result: Even with a positive test, there’s only an 8.8% chance of having the disease!

This is due to the low base rate of the disease

Common Probability Mistakes

  • Confusing \(P(A|B)\) with \(P(B|A)\)

Prosecutor’s fallacy is a specific error in interpreting conditional probabilities. Confusing

\(P(\text{Evidence}\mid\text{Innocent}) \quad\text{with}\quad P(\text{Innocent}\mid\text{Evidence})\).

Ex: OJ Simpson Case 2

Common Probability Mistakes

  • Assuming independence when events are dependent

  • Ignoring base rates (as in the medical test example)

Base rate fallacy is when you ignore or underweight the prior probability \(P(H)\) of a hypothesis, focusing only on the new evidence \(E\).

  • Double counting in union calculations

Practice Problem 3

Two fair dice are rolled. Find:

  1. \(P(\text{sum} = 7)\)
  2. \(P(\text{sum} = 7 | \text{first die shows 3})\)
  3. Are these events independent?

Solution.

  1. 6 ways out of 36: \(P(\text{sum} = 7) = \frac{6}{36} = \frac{1}{6}\)

  2. Given first die is 3, need second die to be 4: \(P(\text{sum} = 7 | \text{first} = 3) = \frac{1}{6}\)

  3. Yes, they’re independent since \(P(A|B) = P(A)\)

Counting and Probability

Sometimes we need to count outcomes:

Multiplication Principle: If task 1 can be done in \(m\) ways and task 2 in \(n\) ways, both can be done in \(m \times n\) ways

Permutations: Arrangements where order matters \[P(n,r) = \frac{n!}{(n-r)!}\]

Combinations: Selections where order doesn’t matter \[C(n,r) = \binom{n}{r} = \frac{n!}{r!(n-r)!}\]

Counting Example

Q: How many ways can you arrange 5 people in a row?

Solution. This is a permutation: \(P(5,5) = 5! = 120\) ways

Q:How many ways can you choose 3 people from 5 for a committee?

Solution. This is a combination: \(C(5,3) = \binom{5}{3} = \frac{5!}{3!2!} = 10\) ways

Probability with Counting

Example: A committee of 3 people is chosen from 8 people (5 women, 3 men). What’s the probability all 3 are women?

Solution. Total ways to choose 3 from 8: \(\binom{8}{3} = 56\)

Ways to choose 3 women from 5: \(\binom{5}{3} = 10\)

Probability: \(\frac{10}{56} = \frac{5}{28}\)

Real-World Applications

Medical Diagnosis: Using Bayes’ theorem for test interpretation

Quality Control: Probability of defective items

Finance: Risk assessment and portfolio theory

Sports: Probability of wins, fantasy sports

Insurance: Calculating premiums based on risk

Key Formulas Summary

  • Basic probability: \(P(A) = \frac{\text{favorable outcomes}}{\text{total outcomes}}\)
  • Complement: \(P(A^c) = 1 - P(A)\)
  • Addition: \(P(A \cup B) = P(A) + P(B) - P(A \cap B)\)
  • Conditional: \(P(A|B) = \frac{P(A \cap B)}{P(B)}\)
  • Independence: \(P(A \cap B) = P(A) \times P(B)\)
  • Bayes’: \(P(A|B) = \frac{P(B|A) \times P(A)}{P(B)}\)

Problem-Solving Strategy

  1. Identify the sample space and events
  2. Determine if events are independent or mutually exclusive
  3. Choose the appropriate rule or formula
  4. Calculate step by step
  5. Check if your answer makes sense

Practice Problem 4

A bag contains 4 red, 3 blue, and 2 green marbles. Three marbles are drawn without replacement.

Find the probability that: a) All three are red b) No two are the same color c) At least one is blue

Practice Problem 4 Solutions

Solution.

  1. All red: \(\frac{4}{9} \times \frac{3}{8} \times \frac{2}{7} = \frac{24}{504} = \frac{1}{21}\)

  2. Different colors: \(\frac{4 \times 3 \times 2}{9 \times 8 \times 7} \times 3! = \frac{24 \times 6}{504} = \frac{144}{504} = \frac{2}{7}\)

  3. At least one blue: \(1 - P(\text{no blue}) = 1 - \frac{6 \times 5 \times 4}{9 \times 8 \times 7} = 1 - \frac{120}{504} = \frac{384}{504} = \frac{16}{21}\)

Common Questions

Q1.: “Why isn’t \(P(A \cup B) = P(A) + P(B)\) always?”

A: We’d double-count outcomes in both events

Q2.: “How do I know if events are independent?”

A: Check if \(P(A|B) = P(A)\) or if \(P(A \cap B) = P(A) \times P(B)\)

Q3.: “When do I use Bayes’ theorem?”

A: When you want to “reverse” a conditional probability

Q3 note (Bayes Example)

  • Forward: I know my test picks up disease 95% of the time ⇒ \(P(+\mid D)=0.95\).

  • Reverse: I want the chance I really have the disease when the test is positive ⇒ \(P(D\mid +)\).

Looking Ahead

Next lecture:

  • Random Variables and Probability Distributions

  • Discrete vs. continuous random variables

  • Expected value and variance

Final Thoughts

Probability is the foundation of statistics:

  • Helps us quantify uncertainty

  • Provides tools for making decisions with incomplete information

  • Essential for understanding statistical inference

Practice: The key to mastering probability is working through many problems!

Questions?

Office Hours: Thursday’s 11 AM On Zoom (Link on Canvas)

Email: nmathlouthi@ucsb.edu

Next Class: Random Variables and Distributions

Resources

Footnotes

  1. \(P(\neg D \,\wedge\, \text{Negative}) \;=\;P(\neg D)\times P(\text{Negative}\mid \neg D) \;=\;0.99\times0.90 \;=\;0.891\;(89.1\%)\)↩︎

  2. the DNA evidence in the O. J. Simpson trial are a classic example of the prosecutor’s fallacy. Prosecutors highlighted that the chance of a random person matching the crime-scene DNA was “one in 170 million,” then implied (or let the jury infer) that Simpson therefore had a 1 in 170 million chance of being innocent.↩︎